Структурные средние

К средним величинам, кроме степенных средних, относят также моду и медиану. Мода и медиана характеризуют величину варианта, занимающего определенное положение в ранжированном вариационном ряду. Моду и медиану определяют, когда расчет средней невозможен и нецелесообразен.

Медиана лежит в середине ранжированного ряда и делит его пополам.

Ряд, в котором значения признака располагаются в порядке возрастания или убывания, называется ранжированным.

Расчет медианы по несгруппированным данным производится в следующем порядке:

a) расположим индивидуальные значения признака в возрастающем порядке;

б) определяем порядковый номер медианы по формуле

. (6.15)

Этот номер соответствует медианному значению х_Ме для ранжированного ряда с нечетным числом членов.

в) для ранжированного ряда с четным числом членов медиану определяем как среднее арифметическое из 2 смежных вариант:

Ме = 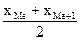. (6.16)

Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.

Формула медианы в интервальном ряду распределения будет иметь следующий вид:

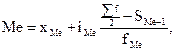(6.17)

где х_Ме – нижняя граница медианного интервала;

i_Ме – величина медианного интервала;

- полусумма частот ряда;

S_Ме-1 – сумма накопленных частот, предшествующих медианному интервалу;

f_Ме – частота медианного интервала.

Медиана может не приближаться ни к одному из наблюдаемых объектов. Медиана находит практическое применение: сумма абсолютных отклонений членов ряда от медианы есть величина наименьшая: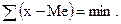

Величины, приходящиеся на одной четверти и на трех четвертях расстояния от начала ряда, называются квартилями, на одной десятой – децилями, а на одной сотой – процентилями.

Мода – наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака. В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, т.е. того интервала, который имеет наибольшую частоту (частость). Значение моды для интервального ряда определяется формулой

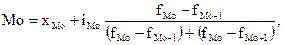(6.18)

где х_Мо – нижняя граница модального интервала;

i_Мо – величина модального интервала;

f_Мо – частота, соответствующая модальному интервалу;

f_Мо-1 – частота, предшествующая модальному интервалу;

f_Мо+1 – частота интервала, следующего за модальным.

При статистическом изучении совокупности правильно выбранная средняя обладает следующими свойствами:

§ если в индивидуальном признаке явления есть какая-либо типичность, то средняя ее обнаруживает, но она учитывает и влияние крайних значений;

§ если 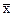, Ме, Мо совпадают, то данная группа симметрична. Но Ме < 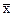при немногочисленной группе с очень высокими числами, и 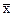< Ме, если нет очень больших чисел и данные концентрируются;

§ если совокупность неоднородна, то мода трудно определяется. Мо < 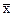, если имеется немногочисленная группа с высокими числами и Мо отчетливо выражена при однородности группы.

Моду и медиану можно определить графически. Медиана определяется по кумуляте. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.

Мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Контрольные вопросы

1. Что представляет собой средняя величина и в чем состоит ее определяющее свойство?

2. Напишите формулу средней арифметической и приведи­те пример исчисления средней по формуле:

а) средней арифметической простой,

б) средней арифметической взвешенной.

3. Назовите основные свойства средней арифметической.

4. Как обосновывается выбор весов при расчете взвешенных средних?

5. Для каких целей используется формула средней геомет­рической?

6. В чем различие между степенными и структурными сред­ними?

7. Использование моды и медианы и их расчет по несгруппированным данным.

Дата добавления: 2015-05-29