IX. Теорема о параллельном переносе силы

Если система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен сумме моментов составляющих относительно того же центра.

VIII. Теорема Вариньона.

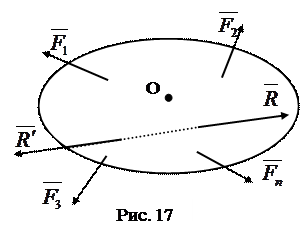Пусть (рис. 17) система 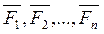имеет равнодействующую 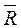. Приложим к телу силу 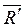=- 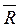, тогда система 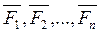, 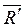~ 0, следовательно сумма моментов всех сил системы, относительно любого центра О, будет равна 0, т.е.

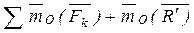=0.

но: 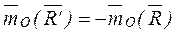, тогда: 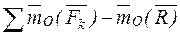= 0. следовательно: 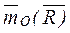= 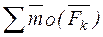. Что и требовалось доказать.

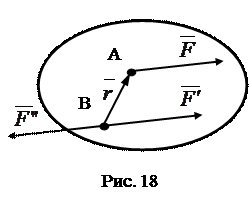Силу можно переносить из данной точки в любую другую, добавляя при этом, пару сил с моментом равным моменту переносимой силы относительно новой точки приложения.

Доказательство (рис.18): Пусть в точке А приложена сила 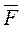. Приложим в точке В силы и 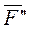, равные, параллельные силе 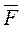, и направленные в противоположные стороны (это можно сделать по первой аксиоме). Тогда систему сил 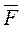, , 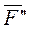можно рассматривать как силу равную 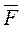и приложенную в точке В, и пару сил 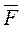, 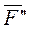момент которой равен моменту силы 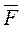относительно точки В: 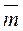(, 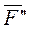) = = 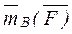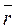× 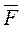. Что и требовалось доказать.

Дата добавления: 2015-06-04