Пример 5. Решить уравнение в целых числах:

Пример 4.

Пример 3.

Пример 2.

Пример 1.

Решить уравнение в целых числах:

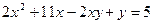
Решение:

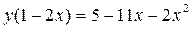
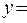
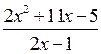
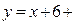
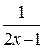
Т.к. уравнение 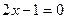не имеет корней в целых числах, то потери корней нет.

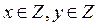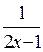Т.к. , то - должно быть целым числом, т.е.

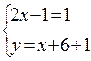или 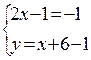Получим: 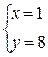или 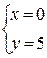Ответ: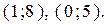

Решить в целых числах уравнение:

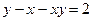
Решение:

Выразим у через х из равенства

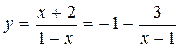
Т.к. 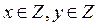, то 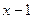может равняться 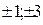, откуда

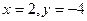
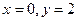
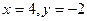
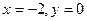
Ответ: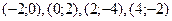

Решить в целых числах уравнение

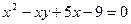
Решение:

,

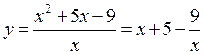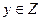
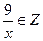, если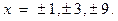

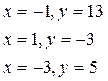
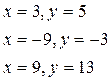
Ответ: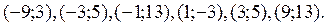

Решить в целых числах уравнение

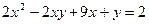
Решение:

Выразим 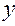через : .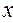

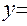
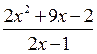Преобразуем полученную дробь

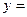
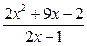
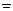
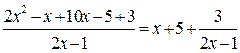
Поскольку 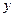и 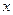– целые, то 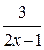должно быть целым числом.

Имеем четыре возможности:

1)

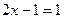
2)

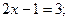
3)

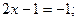
4)

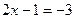
Затем находим 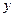и .

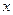Ответ: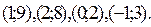

Решить уравнение в целых положительных числах

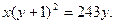
Решение:

Перепишем данное уравнение в виде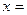

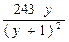
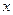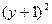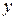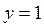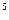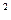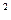Для того, чтобы было целым числом, знаменатель должен быть одним из делителей числа 243, потому что не может иметь общих множителей числа с . Поскольку 243 = 3 , то 243 делится только на следующие числа, являющиеся точными квадратами: 1 , 3 , 9 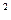. Таким образом 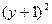может быть равно 1, 9 или 81, откуда находим два решения

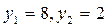. Значит, ,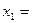

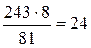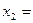
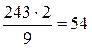
Итак, задача имеет два решения

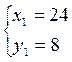
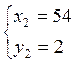
Ответ: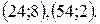

3. Уравнения, решаемые с помощью введения новой переменной.

Пример 1. Найти все положительные числа 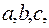для которых

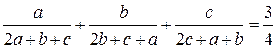
Решение:

Введем обозначения: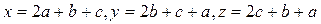

Тогда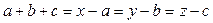

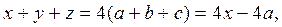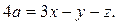и поскольку то И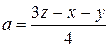

Аналогично получаем выражения для 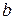и :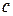

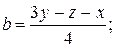
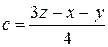
После подстановки этих выражений в равенство, последнее примет вид:

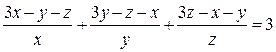
Поделив почленно числители на знаменатели, придем к уравнению:

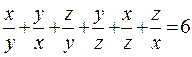
Т.к. сумма взаимно обратных положительных чисел не меньше 2 и равна 2 только в случае их равенства, то 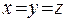, тогда 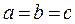. Поэтому заданное равенство выполняется при любых равных положительных числах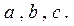

Дата добавления: 2015-07-02