Пример 2. Решить уравнение в простых числах

Пример 1.

Пример 5.

Решить уравнение в простых числах

.

Решение:

Т.к. 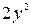- четное число, то 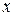– нечётное, и потому число 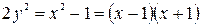делится на 4. Следовательно, 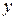- четное число, и поскольку 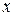и 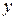должны быть простыми числами, то , а потому .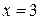

Ответ: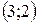

7. Учет четности и нечетности выражений.

Доказать, что не существует решений у уравнения:

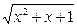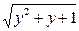+ = 13

Решение:

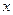
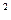
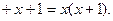Т.к. 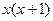– четное, то 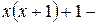нечетное. Корень из нечетного числа – число нечетное.

Аналогично и 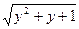- нечетное число. Сумма двух нечетных чисел четно, т.е. в левой части мы имеем число четное, а в правой – нечетное.

Ответ: решений нет.

Найти все пары простых чисел 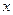и 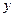, которые удовлетворяют уравнению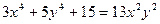

Решение:

1) Если хотя бы одно из чисел 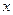или 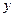четное, то справа будет стоять число четное, при этом, стоящее слева тоже обязано быть четным, а это возможно только в том случае, когда только одно из чисел четно.

2) Пусть (это единственное простое четное число), тогда непосредственно, решив биквадратное уравнение относительно 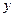, находим 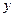= 3.

3) Пусть 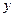=2, непосредственно убеждаемся, что в этом случае натуральных значений 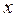, удовлетворяющих уравнению, не существует.

4) Если 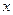и 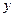– нечетные числа: 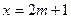и 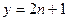, то левая часть первоначального уравнения при делении на 4 дает в остатке 3, при этом правая часть делится на 4 с остатком 1. Следовательно, не существует нечетных простых чисел, удовлетворяющих данному уравнению.

Ответ: .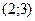

Дата добавления: 2015-07-02