
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сравнение бесконечно малых функций
|
|
|
|
Пример 1.
Одно свойство логарифма и предела функции.
Малых функций.
Примеры.
Вычислить 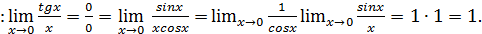
Вычислить:  .
.
Лекция18. Второй классический предел. Сравнение бесконечно
Теорема. Функция y = (1+  имеет предел при
имеет предел при  и он равен
и он равен  2,71828.
2,71828.
Доказательство. Нарисуем график функции y=  .
.
y tg  =
=  , если h
, если h  то
то  0
0
tg 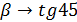 0
0  , то есть
, то есть 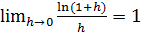
. B  , с другой стороны
, с другой стороны
450 
 , таким образом
, таким образом
0 1. A hc x 
Пусть  , тогда при h
, тогда при h  ,
,  и получим
и получим
ещё одну форму этого предела 
Если существует  , то
, то 
Пользуясь вторым классическим пределом, вычислить:  x+3.
x+3.
Решение.  x+3 =
x+3 =  x+3=
x+3=  x+3=
x+3=  (x+3) 4 (x-1) / 4 (x-1) =
(x+3) 4 (x-1) / 4 (x-1) =  =
= 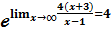 =
=  Ответ:
Ответ: 
Пример 2. Вычислить: 
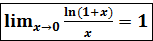
Сравнить две бесконечно малые функции  – это значит, найти предел их отношения при x
– это значит, найти предел их отношения при x 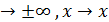 0.
0.
Пусть  – б.м.функции.
– б.м.функции.
1. Функции  называются б. м. одного и того же порядка малости, если
называются б. м. одного и того же порядка малости, если  = c =const
= c =const 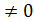 .
.
Пример. Сравнить функции: 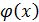 = x2-4 и
= x2-4 и 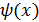 = x2-5x +6при x
= x2-5x +6при x 
Решение. 
Вывод. Функции 
 одного и того же порядка малости.
одного и того же порядка малости.
2. Функция 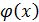 называется б.м. более высокого порядка малости чем
называется б.м. более высокого порядка малости чем 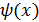 , если
, если  = 0.
= 0.
Пример. Сравнить функции 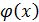 =
=  и
и 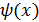 = x при x
= x при x  .
.
Решение.  .
.
Вывод. Функция 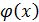 более высокого порядка малости чем функция
более высокого порядка малости чем функция 
3. Функция 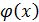 называется б.м. более низкого порядка малости чем
называется б.м. более низкого порядка малости чем  если
если
 .
.
4. Функции 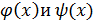 называются не сравнимыми,если
называются не сравнимыми,если  не существует. 69
не существует. 69
Пример. Пусть 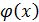 =
=  ,
,  , x
, x  .
.
Решение.  =
=  , не сущуствует.
, не сущуствует.
Вывод. Функции 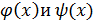 не сравнимы.
не сравнимы.
5. Две функции 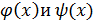 называются эквивалентными или равносильными, если
называются эквивалентными или равносильными, если  =1. Обозначается
=1. Обозначается 
Пример. Вычислить  =
= 
Вывод. arcsinx 

Можно показать, что arctg x  .
.
Составим таблицу эквивалентных функций: при x 
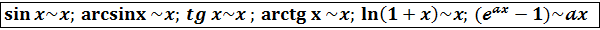
Теорема. Предел отношения 2-х б.м. функций равен пределу отношения эквивалентных им функций.
Доказательство. Пусть  . Докажем, что
. Докажем, что  . Имеем
. Имеем 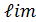



 ]=
]= 

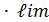
 =
=  ч.т.д. 1
ч.т.д. 1
Замечание.Под знаком предела можно заменять функции им эквивалентными.
Примеры. Вычислить:  1/2x =
1/2x =  =
=  =
= 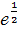 .
.

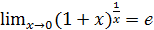 .
.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 77; Нарушение авторских прав?; Мы поможем в написании вашей работы!