Производная второго порядка от неявных функций

Производные высших порядков

Дифференцирование сложно - показательной функции

Определение. Сложно – показательной функцией называется функция, у которой и основание и показатель степени являются функциями от x, например:

(sin x ; ; ; ( Обозначается y = [u(x) = .

Теорема. Если y = , то .

Доказательство. Прологарифмируем функцию y, затем дифференцируем последнее равенство по правилу дифференцирования неявной функции ( → из этого равенства выразим y’.

Y’ = y [ v’ ч.т.д.

Пример1. Найти y’, если y = (sin x

Логарифмируем обе части равенства , дифференцируем = 2x + y’ = y [2x ]

Ответ. Y’ = (sin x 2x ].

Пример 2. Найти y’, если y =

Решение. Сначала найдём логарифм данной функции , дифференцируем обе части, получим

y’ = y[ ]

Ответ. Y’ = [ ].

Приём для нахождения производной с применением логарифмирования называется логарифмическим дифференцированием, а выражение - логарифмической производной.

Так как f’(x) есть функция, то её можно снова дифференцировать.

Определение. Производная от 1-ой производной функции называется производной 2-го порядка.

Определение. Производной n-го порядка функции y = f(x) называется первая производная от производной (n-1) – го порядка. Обозначается: y⁽ⁿ⁾, f⁽ⁿ⁾,

F⁽ⁿ⁾(x) = [ f^(n-1)(x)]’.

Пример. Найти производную - четвёртого порядка для функции y = .

Решение. Сначала найдём y’.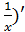

Y’ = , y’’ = ( =- ; y’’’ = (- = = ; y’’’’ =(.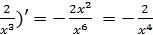

Ответ.

Рассмотрим на примере.

Пример. Найти производную второго порядка от функции y, заданной неявно

x =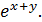

Решение. Дифференцируем обе части равенства, предполагая, что y сложно зависит от x. 1 = , выражаем отсюда y’, y’= ещё раз дифференцируем y’’ = = = =

= .

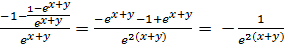Другой способ. Первый раз дифференцируем уравнение, задающее функцию,

получаем 1 = , снова дифференцируем это равенство, 0 = , отсюда выражаем y’’. Y’’ = - (1+y’ , подставляем значение для y’, y’’ = - (1 + = - ( = -

Дата добавления: 2017-02-01