Лекция 24. Дифференциал функции.

Производные функций, заданных параметрически

Механический смысл производной второго порядка

Пусть s = f(t) – путь, пройденный материальной точкой за время t, v = v(t) – скорость за это время, точке t + соответствует скорость v₁(t+ ,

, ускорение

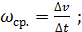
Определение. Ускорением за время t называется предел среднего ускорения при

Вывод. Ускорение прямолинейного движения точки равно второй производной пути по времени.

Пусть , а имеют производные, причём t = , тогда y= сложная функция, поэтому y’_x = _{t x}, на основании теоремы о дифференцировании обратной функции запишем _x = подставим в y’_x = _t = . .

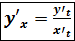Чтобы найти вторую производную, воспользуемся формулой для первой производной, обозначим , .

Можно находить вторую производную по другой формуле

Пример. Найти вторую производную от функции y, заданную параметрически

x = si ; y = sin 2t

Решение. Найдём сначала y’_x. y’_x = = ; y’’_xx = =

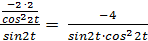= . Ответ. y’’_xx =

Пусть функция y = f (x) дифференцируема на некотором интервале, тогда

Y’ = по теореме ( о пределе функции, имеем

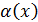→ б.м.функция, при ,

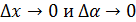, f’(x) поэтому f’(x) 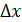- б.м. 1-го порядка малости относительно 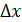. Проверим, какого порядка малости 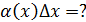Найдём = 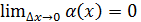, то есть 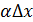более высокого порядка малости, чем 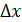. 1- е слагаемое f’(x) называется главной частью приращения функции.

Определение. Дифференциалом функции называется главная часть приращения функции, линейная относительно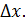

Обозначается . Если y= f(x) = x, то y’_x = 1, а

Вывод. Дифференциал независимой переменной равен приращению этой переменной , 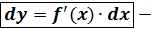рабочая формула.

Пример. Найти дифференциал функции y = .

Решение. f’(x) = , dy = dx.

Приближённые вычисления с помощью дифференциала функции

Запишем приращение функции y = f(x) 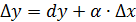, так как последнее слагаемое более высокого порядка, то его отбросим и получим или

F (x₀ + 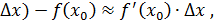отсюда - формула для приближённого вычисления с помощью дифференциала функции.

Пример. Вычислить sin 46⁰.

Решение. Пусть f(x) = sin x; f’(x) = cos x;sin(x+

Примемx₀ + 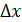= 46⁰; x₀ = , тогда ⁰ =

Sin46⁰ = sin ( = .

Ответ. Sin46⁰ .

Дата добавления: 2017-02-01