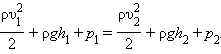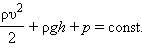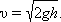КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Циркуляция
|
|
|
|
Простейшие потенциальные течения. Метод наложения потенциальных потоков. Обтекание цилиндра.
Потенциал и его свойства.
Эта величина, сопряженная с величиной и + iv, называется комплексной скоростью и обозначается через W. Очевидно, что w является аналитической функцией от z или от F, следовательно, отображение плоскости ФФ на плоскость uv также является конформным. Существуют такие случаи, когда, не зная функции F(z), определяющей поток в плоскости ху, можно тем не менее заранее, на основании заданных граничных и других условий, построить картину распределения комплексной скорости w в плоскости uv.
Так, например, при истечении жидкости через щель между двумя стенками (рис. 60а) заранее известны направления скорости на стенках аЪ и cd; далее известно, что на границах свободной струи скорость постоянна (это следует из уравнения Бернулли, так как на границах струи давление одинаковое); наконец, нам известны предположительные направления линий тока до истечения из щели, а также предположительное направление струи после истечения. На основании этих данных мы можем построить в плоскости uv картину распределения скоростей и рассматривать ее как некоторый поток. Если для этого потока функция
F = F(w),
его определяющая, известна, то можно путем обращения найти функцию
w = w{F).
Наконец, отделив вещественную и мнимую части комплексной переменной z, мы найдем для каждого значения Ф и Ф соответствующие им значения х. у, т.е. построим картину линий тока.
Приведенных примеров достаточно, чтобы дать представление о применении методов теории функции комплексной переменной в гидродинамике.
Потенциальное течение с циркуляцией. Подъемная сила крыла. Эффект Магнуса. Хотя при всех потенциальных течениях циркуляция в любой малой области потока равна нулю, тем не менее существуют такие потенциальные потоки, в которых циркуляция для всего потока в целом не равна нулю. Правда, необходимым условием для этого является многосвязность области, в которой происходит течение. Область пространства или плоскости называется многосвязной, если в ней можно провести такие замкнутые кривые, которые нельзя стянуть в точку, не разрывая их, т. е. не выходя за пределы области. Примерами двухсвязной области могут служить комната с колонной посредине или область вокруг кольца.
Пусть поток занимает многосвязную область, в каждой односвязной части которой частицы движутся без вращения, следовательно, в каждой такой части циркуляция равна нулю. Далее, пусть в рассматриваемой области циркуляция вдоль какой-нибудь кривой, которую нельзя стянуть в точку, равна Г. Тогда, как легко доказать, циркуляция вдоль любой другой кривой, которую нельзя стянуть в точку и которая получается из первой непрерывной деформацией, также равна Г. В § 10 мы определили потенциал в заданной точке как значение криволинейного интеграла при интегрировании между фиксированной точкой и заданной точкой.
Поскольку теперь в потоке существуют замкнутые кривые, вдоль которых циркуляция не равна нулю, а имеет некоторое значение Г, то это означает, что потенциал такого потока не является больше однозначным; наоборот, теперь он является многозначным, увеличиваясь при каждом обходе нестягиваемой в точку кривой на величину Г. Простейший плоский поток такого рода определяется потенциалом скоростей Ф = с р, где (р есть центральный угол. Этот потенциал, удовлетворяющий, как легко видеть, уравнению, возрастает при каждом полном обходе замкнутой нестягиваемой в точку кривой ((р2 =
Для г = 0 скорость получается равной бесконечности; поэтому физически такой поток возможен только вне некоторого ядра конечного диаметра. Ядро может быть образовано твердым телом или вращающейся жидкостью (движение которой не является потенциальным), наконец, оно может состоять из другой, более легкой жидкости, не принимающей участия в движении. Примером последнего случая является полый водяной вихрь, в котором вода совершает круговое движение вокруг ядра из воздуха. Под действием силы тяжести свободная поверхность такого полого вихря принимает форму. Уравнение этой поверхности получается путем применения уравнения Бернулли к двум линиям тока
Подобного рода воронки часто наблюдаются в реках, в ваннах (при спуске воды) и т.д. Во всех таких случаях мы имеем дело с потоками, в которых циркуляция уже существует и вызвана какими-то посторонними причинами. Другим примером потенциального потока с циркуляцией является поток около крыла самолета. Этот поток получатся из обычного потенциального потока без циркуляции путем наложения на последний циркуляционного потока, вследствие чего при обтекании крыла также возникает циркуляция.
С циркуляцией тесно связано возникновение подъемной силы крыла. Без всякого расчета легко видеть, что при наложении циркуляционного потока на обычный потенциальный поток (рис. 64) скорость последнего над крылом увеличивается, а под крылом, наоборот, уменьшается. Согласно уравнению Бернулли это означает, что над крылом давление уменьшается, а под крылом увеличивается, следовательно, возникает сила, действующая на крыло снизу вверх, т. е. подъемная сила. Кут-та (Kutta) и Н. Е. Жуковский независимо друг от друга1 нашли путем теоретических расчетов, что подъемная сила на единицу длины крыла равна А = pTV, где р есть плотность жидкости, Г — циркуляция, aV — относительная скорость крыла и жидкости. Следовательно, подъемная сила прямо пропорциональна циркуляции. Вывод указанной формулы будет дан ниже
Если движение начинается из состояния покоя, то, согласно теореме Томсона, в получившемся потоке циркуляция не может возникнуть даже в том случае, когда движение происходит в многосвязной области. В самом деле, в состоянии покоя циркуляция вдоль всякой замкнутой кривой равна нулю, поэтому она должна остаться равной нулю и после начала движения. В действительности же циркуляция, как правило, возникает, и причиной этого является образование поверхности раздела. Так, например, в спиральной камере, в первый момент начала движения образуется на остром ребре к поверхность раздела, из которой возникает вихрь такого же вида.
В дальнейшем вихрь отрывается от ребра и уплывает вместе с потоком, но вызванная им циркуляция остается в потоке на все время. Совершенно аналогичная картина наблюдается и при движении крыла. В начале движения поток под крылом огибает заднюю кромку крыла снизу вверх, вследствие чего здесь образуется поверхность раздела, превращающаяся в вихрь. В дальнейшем вихрь отрывается от крыла и уплывает вместе с потоком, но оставляет в нем циркуляцию, равную по абсолютной величине своей циркуляции, но противоположно направленную.
При этом вдоль жидких линий, заключающих внутри себя крыло и вихрь вместе, циркуляция остается равной нулю, как этого и требует теорема Томсона. Для того чтобы от присутствия крыла область пространства сделалась двухсвязной, необходимо, чтобы крыло с боков было ограничено двумя параллельными стенками или чтобы крыло простиралось в обе стороны до бесконечности. Для действительных крыльев ни одно из этих условий не соблюдается. Тем не менее циркуляция, без которой не может получиться подъемная сила, возникает и в этом случае. Она возникает вследствие отрыва вихрей, образующихся из поверхности раздела с поперечным скачком скорости Если на вращающийся круглый цилиндр набегает поток воздуха в направлении, перпендикулярном к оси цилиндра, то вокруг него возникает циркуляция такого же вида, как и вокруг крыла. В дальнейшем, мы увидим, что причиной возникновения этой циркуляции является трение.
Циркуляция вокруг цилиндра создает силу, действующую на цилиндр в направлении, перпендикулярном к направлению потока, и называемую поэтому поперечной силой. На единицу длины оси цилиндра эта сила равна, как и при циркуляции вокруг крыла, pTV. Такая же сила возникает и при набегании потока на трехгранную или четырехгранную призму, вращающуюся вокруг продольной оси, на вращающийся шар и т. д. Направлена поперечная сила всегда к той стороне вращающегося тела, на которой направление вращения и направление потока совпадают. Возникновение при указанных условиях поперечной силы называется, по имени ученого Магнуса (Magnus), впервые открывшего (в 1852 г.) это явление, эффектом Магнуса.
До изобретения нарезных артиллерийских орудий часто случалось, что шаровые снаряды после вылета из ствола значительно отклонялись в сторону от той траектории, по которой они должны были бы лететь. Магнус показал, что причиной такого поведения снаряда служило вращение вокруг поперечной оси, которое шаровой снаряд получал вследствие случайных причин. На основании сказанного выше это создавало условия, необходимые для возникновения поперечной силы, которая и вызывала нежелательное отклонение снаряда от намеченной траектории. Такие же боковые отклонения, часто очень значительные, наблюдаются и при полете «срезанного» мяча при игре в теннис или гольф. Несколько лет тому назад А. Флеттнер (Flettner) использовал эффект Магнуса для приведения в движение корабля энергией ветра, причем вместо парусов он установил вертикальные быстро вращающиеся цилиндры (роторы).
На концах цилиндров помещались выступающие круглые диски, так как иначе воздух, расположенный выше и ниже цилиндра, засасывался в область потока с пониженным давлением и, возмущая поток, уменьшал поперечную силу. Испытания показали техническую пригодность такого роторного корабля, но в экономическом отношении он оказался менее выгодным обычных моторных судов и поэтому не получил дальнейшего применения. Эффект Магнуса можно продемонстрировать при помощи следующего опыта. Поставим на рельсы легкую тележку с вертикальным цилиндром, приводимым во вращение маленьким электромоторчиком, и начнем обдувать этот цилиндр потоком воздуха, направленным поперек рельсов (для получения такого потока можно воспользоваться настольным вентилятором). Тележка сейчас же начнет двигаться вдоль рельсов. Устанавливая вентилятор так, чтобы поток воздуха набегал на цилиндр под непрямым углом к направлению рельсов, можно исследовать движение цилиндра-паруса на разных курсах. Можно даже заставить тележку катиться против ветра под острым углом. При перемене направления вращения цилиндра тележка катится в обратную сторону.
Можно произвести также следующий опыт. Приведем в быстрое вращение легкий цилиндр, расположив при этом его ось горизонтально, и предоставим цилиндру падать. Мы увидим, что вместо того, чтобы упасть вертикально вниз, цилиндр начнет планировать по довольно пологой траектории. При таком движении на цилиндр, кроме подъемной (поперечной) силы А, перпендикулярной к направлению движения, действует еще сопротивление W, направленное против движения, которое, однако, в случае длинного и узкого цилиндра и при наличии боковых дисков значительно меньше, чем подъемная сила. Равнодействующая этих обеих сил уравновешивает вес цилиндра и тем самым замедляет его падение.

Элементы гидро- и аэродинамики window.top.document.title = "1.22. Элементы гидро- и аэродинамики";
Движение жидкостей или газов представляет собой сложное явление. Для его описания используются различные упрощающие предположения (модели). В простейшей модели жидкость (или даже газ) предполагается несжимаемыми и идеальными (т. е. без внутреннего трения между движущимися слоями). При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии. Следствием этого закона для стационарного потока идеальной и несжимаемой жидкости является уравнение Бернулли, сформулированное в 1738 г. Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.
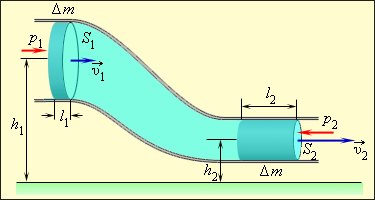
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения (рис. 1.22.1). Различные части трубы могут находиться на разных высотах.
|
| Рисунок 1.22.1. Течение идеальной жидкости по трубе переменного сечения. ΔV1 = l1S1; ΔV2 = l2S2. Условие несжимаемости: ΔV1 = ΔV2 = ΔV |
За промежуток времени Δt жидкость в трубе сечением S1 переместится на l1 = υ1Δt, а в трубе сечением S2 – на l2 = υ2Δt, где υ1 и υ2 – скорости частиц жидкости в трубах. Условие несжимаемости записывается в виде:
| ΔV = l1S1 = l2S2 или υ1S1 = υ1S1. |
Здесь ΔV – объем жидкости, протекшей через сечения S1 и S2.
Таким образом, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется с ускорением. Следовательно, на жидкость действует сила. В горизонтальной трубе эта сила может возникнуть только из-за разности давлений в широком и узком участках трубы. Давление в широком участке трубы должно быть больше чем в узком участке. Если участки трубы расположены на разной высоте, то ускорение жидкости вызывается совместным действием силы тяжести и силы давления. Сила давления – это упругая сила сжатия жидкости. Несжимаемость жидкости означает лишь то, что появление упругих сил происходит при пренебрежимо малом изменении объема любой части жидкости.
Так как жидкость предполагается идеальной, то она течет по трубе без трения. Поэтому к ее течению можно применить закон сохранения механической энергии.
При перемещении жидкости силы давления совершают работу:
| ΔA = p1S1l1 – p2S2l2 = p1S1υ1Δt – p2S2υ2Δt = (p1 – p2)ΔV. |
Работа ΔA сил давления равна изменению потенциальной энергии упругой деформации жидкости, взятому с обратным знаком.
Изменения, произошедшие за время Δt в выделенной части жидкости, заключенной между сечениями S1 и S2 в начальный момент времени, при стационарном течении сводятся к перемещению массы жидкости Δm = ρΔV (ρ – плотность жидкости) из одной части трубы сечением S1 в другую часть сечением S2 (заштрихованные объемы на рис. 1.22.1). Закон сохранения механической энергии для этой массы имеет вид:
| E2 – E1 = ΔA = (p1 – p2)ΔV, |
где E1 и E2 – полные механические энергии массы Δm в поле тяготения:
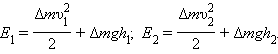
|
Отсюда следует:
|
Это и есть уравнение Бернулли. Из него следует, что сумма
|
остается неизменной вдоль всей трубы. В частности, для горизонтально расположенной трубы (h1 = h2) уравнение Бернулли принимает вид:
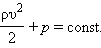
|
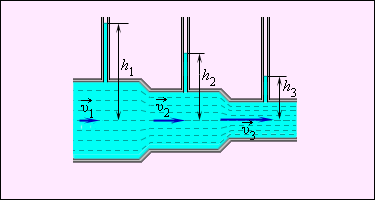
Величина p – статическое давление в жидкости. Оно может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. 1.22.2). Из уравнения Бернулли следует:
Давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, и наоборот, давление меньше в тех сечениях, в которых скорость больше.
|
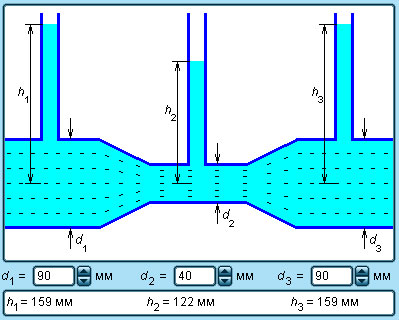
| Рисунок 1.22.2. Измерение давления в потоке жидкости с помощью манометров. υ1 < υ2 < υ3; h1 > h2 > h3 |

|
| Модель. Течение идеальной жидкости |
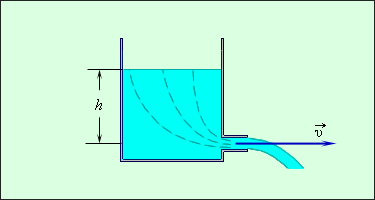
Если сечение потока жидкости достаточно велико, то уравнение Бернулли следует применять к линиям тока, т. е. линиям, вдоль которых перемещаются частицы жидкости при стационарном течении. Например, при истечении идеальной несжимаемой жидкости из отверстия в боковой стенке или дне широкого сосуда линии тока начинаются вблизи свободной поверхности жидкости и проходят через отверстие (рис. 1.22.3).
|
| Рисунок 1.22.3. Истечение жидкости из широкого сосуда |
Поскольку скорость жидкости вблизи поверхности в широком сосуде пренебрежимо мала, то уравнение Бернулли принимает вид:

|
где p0 – атмосферное давление, h – перепад высоты вдоль линии тока. Таким образом,
|
Это выражение для скорости истечения называют формулой Торричелли. Скорость истечения идеальной жидкости из отверстия в сосуде такая же, как и при свободном падении тела с высоты h без начальной скорости.
В отличие от жидкостей, газы могут сильно изменять свой объем. Расчеты показывают, что сжимаемостью газов можно пренебречь, если наибольшие скорости в потоке малы по сравнению со скоростью звука в этом газе. Таким образом, уравнение Бернулли можно применять к достаточно широкому классу задач аэродинамики.
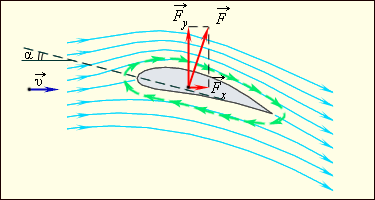
Одной из таких задач является изучение сил, действующих на крыло самолета. Строгое теоретическое решение этой задачи чрезвычайно сложно, и обычно для исследования сил применяются экспериментальные методы. Уравнение Бернулли позволяет дать лишь качественное объяснение возникновению подъемной силы крыла. На рис. 1.22.4 изображены линии тока воздуха при обтекании крыла самолета. Из-за специального профиля крыла и  наличия угла атаки, т. е. угла наклона крыла по отношению к набегающему
наличия угла атаки, т. е. угла наклона крыла по отношению к набегающему  потоку
потоку  воздуха, скорость воздушного
воздуха, скорость воздушного  потока
потока  над крылом оказывается больше, чем под крылом. Поэтому на рис. 1.22.4 линии тока над крылом располагаются ближе друг к другу, чем под крылом. Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила
над крылом оказывается больше, чем под крылом. Поэтому на рис. 1.22.4 линии тока над крылом располагаются ближе друг к другу, чем под крылом. Из уравнения Бернулли следует, что давление в нижней части крыла будет больше, чем в верхней; в результате появляется сила 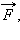 действующая на крыло. Вертикальная составляющая
действующая на крыло. Вертикальная составляющая  этой силы называется подъемной силой. Подъемная сила позволяет скомпенсировать силу тяжести, действующую на самолет,
этой силы называется подъемной силой. Подъемная сила позволяет скомпенсировать силу тяжести, действующую на самолет,  и
и  тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая
тем самым она обеспечивает возможность полета тяжелых летательных аппаратов в воздухе. Горизонтальная составляющая 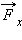 представляет собой силу сопротивления среды.
представляет собой силу сопротивления среды.
|
Рисунок 1.22.4.
Линии тока при  обтекании обтекании  крыла самолета крыла самолета  и и  возникновение подъемной силы. α – угол атаки возникновение подъемной силы. α – угол атаки
|
Теория подъемной силы крыла самолета была создана Н. Е. Жуковским.  Он
Он  показал, что при
показал, что при  обтекании
обтекании  крыла существенную роль играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение (циркуляция) воздуха вокруг крыла (зеленые стрелки на рис. 1.22.4). В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего
крыла существенную роль играют силы вязкого трения в поверхностном слое. В результате их действия возникает круговое движение (циркуляция) воздуха вокруг крыла (зеленые стрелки на рис. 1.22.4). В верхней части крыла скорость циркулирующего воздуха складывается со скоростью набегающего  потока
потока  , в нижней части эти скорости направлены в противоположные стороны. Это
, в нижней части эти скорости направлены в противоположные стороны. Это  и
и  приводит к возникновению разности давлений
приводит к возникновению разности давлений  и
и  появлению подъемной силы.
появлению подъемной силы.
Циркуляция воздуха, обусловленная силами вязкого трения, возникает  и
и  вокруг вращающегося тела (например,
вокруг вращающегося тела (например,  цилиндра
цилиндра  ). При вращении
). При вращении  цилиндр
цилиндр  увлекает прилегающие слои воздуха, вызывая
увлекает прилегающие слои воздуха, вызывая  его
его  циркуляцию. Если такой
циркуляцию. Если такой  цилиндр
цилиндр  установить в набегающем
установить в набегающем  потоке
потоке  воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса. Рис. 1.22.5 иллюстрирует
воздуха, то возникнет сила бокового давления, аналогичная подъемной силе крыла самолета. Это явление называется эффектом Магнуса. Рис. 1.22.5 иллюстрирует  обтекание
обтекание  вращающегося
вращающегося  цилиндра
цилиндра  набегающим
набегающим  потоком
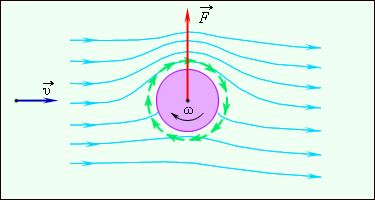
потоком  . Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в теннис или футбол.
. Эффект Магнуса проявляется, например, при полете закрученного мяча при игре в теннис или футбол.
|
Рисунок 1.22.5.
 Обтекание Обтекание  вращающегося вращающегося  цилиндра цилиндра  набегающим набегающим  потоком потоком  воздуха воздуха
|
Итак, во многих явлениях аэродинамики существенную роль играют силы вязкого трения. Они приводят к возникновению циркулирующих потоков воздуха вокруг крыла самолета или вокруг вращающегося тела, к появлению силы сопротивления среды и т. д. Уравнение Бернулли не учитывает сил трения. Его вывод основан на законе сохранения механической энергии при  течении
течении  жидкости или газа. Поэтому с помощью уравнения Бернулли нельзя дать исчерпывающего объяснения явлений, в которых проявляются силы трения. В этих случаях можно руководствоваться только качественными соображениями – чем больше скорость, тем меньше давление в потоке газа.
жидкости или газа. Поэтому с помощью уравнения Бернулли нельзя дать исчерпывающего объяснения явлений, в которых проявляются силы трения. В этих случаях можно руководствоваться только качественными соображениями – чем больше скорость, тем меньше давление в потоке газа.
Особенно заметно проявляются силы вязкого трения при течении жидкостей. У некоторых жидкостей вязкость настолько велика, что применение уравнение Бернулли может привести к качественно неверным результатам. Например, при истечении вязкой жидкости через отверстие в стенке сосуда ее скорость может быть в десятки раз меньше рассчитанной по формуле Торричелли. При движении сферического тела в идеальной жидкости оно не должно испытывать лобового сопротивления. Если же такое тело движется в вязкой жидкости, то возникает сила сопротивления, модуль которой пропорционален скорости υ и радиусу сферы r (закон Стокса)
|
Коэффициент пропорциональности в этой формуле зависит от  свойств жидкости.
свойств жидкости.
Поэтому, если тяжелый шарик бросить в высокий сосуд, наполненный вязкой жидкостью (например, глицерином), то через некоторое время скорость шарика достигнет установившегося значения, которое не будет изменяться при дальнейшем движении шарика. При движении с установившейся скоростью силы, действующие на шарик (сила тяжести 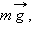 выталкивающая сила
выталкивающая сила 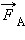 и сила сопротивления среды
и сила сопротивления среды 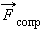 ), оказываются скомпенсированными, и их равнодействующая равна нулю.
), оказываются скомпенсированными, и их равнодействующая равна нулю.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 3295; Нарушение авторских прав?; Мы поможем в написании вашей работы!