Вихревая теория

Вихревые линии, трубки, шнуры. Напряжение вихревого шнура.

, теория вихрей, учение о вихревом движении жидкости, имеющее большие приложения в аэродинамике и гидродинамике и являющееся одной из важнейших глав этих наук. Так как почти во всех действительных гидродинамических явлениях возникают вихри, то приложение теории вихрей к изучению этих явлений имеет большое значение. За последнее время В. т. дала возможность исследовать такие сложные явления, какими являются работа гребного винта (см. Воздушный винт), сопротивление тел (см. Индуктивное сопротивление) и т. п.

Можно показать, что движение малой жидкой частицы составляется: 1) из поступательного движения ц. т. частицы, 2) из движения с потенциалом скоростей, которое выражается в деформациях частицы, и 3) из

вращательного движения частицы (1-я теорема Гельмгольца). Проекции угловой ско>-рости частицы на оси координат будут £, *? и £ (см. Аэродинамика). При равенстве нулю этих компонентов вихря |, j? и £, движение будет с потенциалом скоростей.

Если в жидкости проследить непрерывное изменение направления мгновенных осей вращения частиц и провести линию, касательные к к-рой будут совпадать с этими осями, то такая линия будет называться вихревой линией. Поверхность, проведенная через какую-нибудь линию в жидкости и образованная из вихревых линий, называется вихревой поверхностью. Жидкость, заключенная внутри вихревой поверхности,построенной на бесконечно малом замкнутом контуре, называется вихревой нитью. Если среди неза--вихренной жидкости имеется вихревая область, к-рая заключена в конечной толщины трубку , образованную вихревой поверхностью, то она называется вихревым . шнуром . Если же эта область заключена между двумя близкими вихревыми поверхностями, она называется вихревым слоем. Произведение площади сечения вихревой нити da на угловую скорость вращения жидкости со в этой нити называется напряжением вихревой нити. Напряжение вдоль вихревой нити остается постоянным (2-я теорема Гельмгольца), а отсюда следует, что вихревые нити сами на себя замыкаются или лежат на границах жидкости, ибо если вихревая нить кончилась бы в жидкости острием, то da= О, и ш обратилась быв со. Возьмем в жидкости какой-либо замкнутый контур, спроектируем на касательную в каждой его точке скорость в этой точке v и возьмем по всему контуру сумму произведений этих проекций на элемент контура. Полученное выражение

где «—угол между касательной и направлением скоростей, a ds — элемент контура, называется циркуляцией по данному контуру. Циркуляция играет очень большую роль в В. т., ибо при помощи ее значительно упрощаются нек-рые определения, выводы и ф-лы. Циркуляция аналогична работе в механике, только в ней роль силы играет скорость. По.теореме Стоке а, циркуляция по взятому замкнутому контуру в односвязном пространстве (т. е. в пространстве, в к-ром всякий контур можно обратить в точку) равна удвоенной сумме напряжений всех вихревых нитей, проходящих через площадь, охватываемую контуром. Из этой теоремы следует, что если циркуляция по любому контуру равна нулю, то угловая скорость вращения частиц равна нулю:

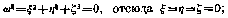
это и есть признак наличия потенциала скоростей и, следовательно, незавихренности.потока. Т. о. в невихревом потоке циркуляция по любому контуру равна нулю. Циркуляция по замкнутому контуру, проводимому через одни и те же частицы жидкости, остается во все время движения постоянной (теорема Томсона). Отсюда следует, что если потенциал скоростей существовал в на-

чальный момент, то он будет существовать и все время, и, наоборот, вихревое движение, раз оно существует, разрушиться не может. Таким образом в идеальной жидкости вихри возникнуть не могут.

Рассмотрим бесконечно длинный прямолинейный вихревой шнур с циркуляцией J, находящийся в среде, в к-рой других вихрей нет. Этот вихревой шнур вызовет вокруг себя определенное поле скоростей; линии токов этого движения будут концен-

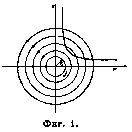
трическ. окружностями, и мы получим т.н.циркуляци-онный поток (фиг. 1), скорости которого найдутся из следующих соображений. Так как вне вихря других вихрей нет, то, следовательно, по теореме Стокса, вокруг этого вихря циркуляция по любому контуру будет равна J. Циркуляция по концентрической вихрю окружности с радиусом г

будет: J=27tvr, откуда скорость

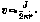
Если

радиус цилиндрического вихря обозначить через г₀ и скорость на поверхности через v₀, то скорость в любой точке вне вихря будет

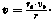
Если принять v за ось ординат, а

г —за ось абсцисс, то это ур-ие представит собою равнобокую гиперболу. Как видим, скорость при небольших г изменяется очень быстро, и при очень тонком шнуре, радиус которого близок к нулю, скорость близка к бесконечности; следовательно, теоретически, около такого бесконечно тонкого вихря получаются бесконечно большие скорости. Давление в каждой точке найдется по ур-ию:

Т. к. с уменьшением радиуса

скорость увеличивается, то внутри вихря будет пониженное давление. Указанный тип вихря встречается в природе в виде смерчей, тайфунов и америк. торнадосов. Вследствие пониженного давления внутри вихря он захватывает с собой встречающиеся по пути его движения предметы. Сравнительно резко ограниченная область больших скоростей и пониженного давления делает путь опустошения смерча также резко очерченным. В случае наличия нескольких прямолинейных вихрей скорость, вызванную ими в какой-нибудь точке жидкости, можно найти, пользуясь принципом независимости действия, согласно которому полная вызванная вихрями скорость равна геоме-трич. сумме скоростей, вызванных отдельными вихрями. В случае криволи-

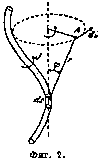
нейных шнуров вызванная элементом вихря ds скорость dv в точке А выражается следующим образом (фиг. 2):

где J —циркуляция вокруг вихря, <р —угол между расстоянием от дайной точки до элемента вихря ds и осью вращения точки А. Эта формула является аналогичной формуле

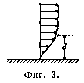
электродинамики, выражающей закон Био-Савара о действии электрического тока на магнитный полюс. Вообще говоря, между электромагнитными и гидродинамическими явлениями наблюдается большая аналогия. Движение вихрей, даже прямолинейных, довольно трудно поддается математич. исследованию вследствие сложности самого явления; эти явления упрощают, рассматривая плоское движение, перпендикулярное оси вихрей. Если принять напршке-ние вихря за его массу, то при наличии нескольких прямолинейных вихрей можно найти их общий ц. т. Если имеются два прямолинейных параллельных вихревых шнура , вращающихся в одну и ту же сторону, то они будут вращаться около общего ц. т.; при вращении в разные стороны они будут двигаться прямолинейно, сохраняя

одинаковые между собой расстояния. Одиночные вихри остаются неподвижными, если нет пере н о с н о го д в и лее и и я. Интересными вихре-образованиями являются вихревые кольца, которые представляют собою вихревые шнуры , замкнутые сами на себя. Эти кольца двигаются по тому направлению, по которому отбрасывается жидкость внутри кольца. Чем тоньше кольцо, тем быстрее при той же циркуляции оно двшкется. Если выпустить одно за другим два вихревых кольца, то будет наблюдаться т. п. игра колец, при которой одно кольцо попеременно догоняет другое и кольца, изменяя свою величину, проходят одно сквозь другое.

Объяснение образования вихрей около обтекаемого жидкостью тела при наличии хотя бы малой вязкости дал в 1904 году Прантль, пользуясь теорией погра-п и ч и о г о слоя. При движении тела в

жидкости, на его поверхности, вследствие трения, скорость равна нулю, возрастая при удалении от поверхности и, наконец, становясь равной окружающему потоку (фиг. 3). Т. о. около тела образуется пограничный слой нек-рой толщины д, скорости в к-ром

отличны от таковых в окружающем потоке и толщина к-рого зависит от вязкости жидкости: чем меньше вязкость, тем меньше его толщина; для идеальной жидкости, без вязкости, толщина этого слоя будет равна нулю. Рассмотрим движение цилиндра (фиг. 4) в вязкой среде. Теоретически в точках А и А' имеется повышенное давление и в точках С и С"—пониженное. Поэтому около поверхности цилиндра получаются течения от Л к С и к С и от А' к С и С"; этими течениями пограничный вихревой слой увлекается, и за точками С и С вследствие получившихся противоположных токов начинают появляться вихри (фиг. 5). При малых

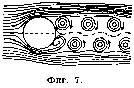
скоростях движения течение получается почти точно симметричное. При увеличении же скорости вихри за цилиндром приобретают известную интенсивность и питаются пограничным слоем, смываемым общим течением (фиг. 6), и за телом образуются два симметрично расположенных вихря. Однако такое расположение парных вихрей не является устойчивым: наличие каких-либо случайных причин, хотя бы в виде сотрясений, ведет к изменению их на вихри, отрывающиеся от цилиндра поочередно и располагающиеся сзади в шахмат, порядке (фиг. 7). Периодич. отрывание таких вихрей наблюдается и при обтекании других тел и может, при известной частоте, произвести слышимый звук (например в органных трубах) или, попадая в резонанс, произвести колебания других систем (напр. вибрации проволок на аэроплане или стабилизатора от вихрей, срывающихся с крыльев аэроплана). Система шахматных вихрей позволила проф. Карману создать вихревую теорию лобового сопротивления.

Таким образом общее сопротивление тела в жидкости состоит из сопротивления,

обусловленного образованием вихрей, и из сопротивления трения.

Гельмгольц вводит понятие вихревой линии. Если мы в определенной точке среды найдем направление мгновенной оси вращения, по ней продвинемся на бесконечно малую длину, найдем новое положение мгновенной оси вращения, по ней снова продвинемся и т.д., то полученная линия и будет вихревой линией.

Если взять какой-нибудь очень маленький контур ds и на нем построить линии вихрей, то получим поверхность в форме весьма тонкой вихревой трубки. Гельмгольц рассматривает массу жидкости, заключенную в этой трубке, и называет ее вихревой нитью (рис.2).

Рис. 1 Рис. 2

Произведение угловой скорости вращения на площадь сечения вихревой нити - wds - Гельмгольц называет напряжением вихревой нити.

Между вихревой нитью и струйкой жидкости есть геометрическое сродство. Если для течения жидкости мы станем строить линии тока и струйки жидкости, то мы заметим, что линии тока суть линии вихрей, а струйки этого воображаемого течения суть вихревые нити действительного течения и объем, протекающий по струйке воображаемого потока в единицу времени - wds - будет равен постоянной величине.

Отсюда получается вторая теорема Гельмгольца о вихрях: вдоль всей вихревой нити напряжение вихря постоянно.

Эта замечательная теорема характеризует вихревые нити: из нее заключаем, что вихревая нить не может оканчиваться острием при непрерывном распределении скоростей. Действительно, если бы вихревая нить заканчивалась острием, как на рис.3, то ds обратилась бы в 0, и w в ¥. Раз это невозможно, то могут быть только два случая: или вихревые нити сами в себе замыкаются, или концы их лежат на границах среды: например, для жидкости, на свободной поверхности, или на стенках сосуда (рис.4).

Рис. 3 Рис. 4

Третья и четвертая теоремы Гельмгольца - теоремы о неразрушимости и неизменности напряжения вихревой нити во все время ее движения

Рассмотрим фундаментальное понятия в теории вихревой нити, которые неразрывно взаимосвязаны и получили название циркуляция скорости и интенсивность вихря I. Циркуляцией скорости по какому-нибудь контуру называется выражение:

I=òVcosqds, (2)

т.е. сумма произведений проекции скорости на касательную к контуру на соответствующий элемент дуги. Это выражение похоже на выражение работы: если бы величина V была силой, то работа этой силы при перемещении точки по контуру выразилась бы той же формулой.

В частном случае, когда существует потенциал скоростей j, проекция скорости на касательную выражается частной производной от потенциальной функции по элементу дуги, и

, (3)

где j₁ и j₀ суть значения потенциала скоростей в начале и в конце контура. Если контур замкнутый, то j₁=j₀ и

I=j₁-j₀=0. (4)

Вследствие произвольности выбора осей координат, вытекает, что циркуляция скорости по бесконечно малому замкнутому элементу равна двойной проекции угловой скорости вращения на нормаль к этому элементу, помноженной на площадь его:

i=2wcosads. (5)

направление контура берется по часовой стрелке для наблюдателя, глядящего с конца нормали на контур.

Теперь перейдем к теореме Стокса (Stokes), опираясь на уравнение (5).

Эта теорема имеет место для контуров, обращающихся в точку, не выходя из среды.

Если пространство односвязно, то таким свойством обладает всякий контур. Например, если представить себе наполненную водой пустую комнату, то какой бы контур в ней не взять, он мог бы, уменьшаясь, обратиться в точку, оставаясь все время внутри жидкости.

Если же в комнате оставить стулья, то можно было бы вообразить контур, охватывающий перекладину стула; такой контур нельзя было бы обратить в точку, и пространство называлось бы многосвязным.

Если контур обладает свойством обратимости в точку, то мы можем через него провести поверхность, которая вся лежит внутри среды, например, жидкости. На этой поверхности построим две системы взаимно ортогональных кривых (рис.5), которые рассекают площадь ее на отдельные элементарные прямоугольники. Очевидно, что циркуляция по внешнему контуру равна сумме циркуляций по отдельным прямоугольникам:

I=åi,

Так как на всякой внутренней стороне прямоугольников будем иметь по две циркуляции в противоположных направлениях, которые взаимно уничтожаются, и останутся только несдвоенные циркуляции, которые идут по внешнему контуру.

Заменяем каждое i через

2wcosads.

Тогда

I=2åwcosads=2òòwcosads. (6)

Если принять угловые скорости вращения частиц жидкости за скорости некоторого течения, то выражение (6) представит объем жидкости, протекающей через рассматриваемый контур. Такой воображаемый поток будет несжимаемым и объем протекающей жидкости I не будет зависеть от выбора поверхности, проведенной через контур. Количество жидкости, протекающей по каждой струйке этого воображаемого потока, представляет не что иное, как напряжение соответственных вихревых нитей действительного потока.

Отсюда вытекает следующая теорема Стокса:

Циркуляция скорости по всякому замкнутому контуру, обращающемуся в точку, не выходя из жидкости, равна удвоенной сумме напряжений всех вихревых нитей, проходящих через контур.

Согласно теореме Стокса интенсивность вихревой трубки равна циркуляции скорости по контуру, на который опирается площадь поперечного сечения трубки.

Приложим теорему Стокса к определению скоростей, которые развивает внутри, например, жидкости находящийся в ней бесконечно длинный вихревой шнур.

Пусть на рис.6 представлен такой шнур ab. Он отмечается тем, что циркуляция скорости, взятая вокруг него, есть величина конечная. Она выражает двойное напряжение этого вихря. Можно рассматривать такой вихревой шнур или весьма тонким с очень большой скоростью вращения, или как цилиндр конечной площади сечения, вращающийся с конечной же скоростью. В остальной части жидкости, вне шнура, вихрей нет, так что мы получаем компоненты скорости вихря только внутри этого цилиндра. В результате линии токов будут симметричны относительно оси вихря и представлять окружности; центры последних лежат на оси вихря, и плоскости их ей перпендикулярны. Циркуляция скорости по каждой такой окружности равна

I=2prV,

где V - скорость жидкости, а r - радиус окружности. Эта циркуляция должна иметь одну и ту же величину для всех окружностей, потому что каждую из них пронизывает один и тот же вихревой шнур. Эта величина равна

I=2pr₀V₀,

где r₀ и V₀ - радиус вихревого шнура и скорость на его поверхности. Отсюда скорость каждой точки

;

т.е. обратно пропорциональна радиусу. Давление

,

т.е. уменьшается с уменьшением r. Поэтому вихревой шнур вследствие пониженного давления притягивает к себе остальные массы; всякое твердое тело, находящееся вне вихревого столба, стремясь двигаться в сторону меньшего давления, будет приближаться к оси вихря.

Если рассматриваемый вихревой шнур заключен между двумя стенками, перпендикулярными к его оси, то на концах его будет пониженное давление, и потому он своими концами присасывается к стенкам.

Рассматриваемые вихревые шнуры в природе представляются в виде смерчей, которые опираются нижними своими концами на землю или воду, а верхними на тучу.

Итак, мы установили основные свойства вихревой нити, а именно:

1. по первой теореме Гельмгольца вихревое движение слагается из поступательного движения, вращательного и движения деформации. Движение деформации имеет потенциал скоростей. бесконечно-малый вихревой шарик, деформируясь, обращается в бесконечно-малый вихревой эллипсоид, причем оси его направлены по осям деформации;
2. по второй теореме Гельмгольца напряжение вихря вдоль всей вихревой нити остается величиной постоянной. Она устанавливает понятие о вихревых линиях и показывает, что они должны или быть замкнутыми или оканчиваться на границах жидкости;
3. по третьей теореме Гельмгольца вихревая нить всегда остается вихревой нитью;
4. по четвертой теореме Гельмгольца напряжение вихревой нити во все время движения одинаково. Предположим, что нарисованная на рис.6 вихревая нить бесконечно тонка, и охватим ее контуром b.

Тогда по теореме Стокса, циркуляция по этому контуру равна двойному напряжению вихревой нити. Так как циркуляция скорости по контуру b не меняется при передвижении рассматриваемой жидкой массы, то не меняется и напряжение вихревой нити, что и требовалось доказать. Тот же вывод следует и для вихревого кольца, рис.7.

Рис. 5 Рис.6 Рис.7

Хотя площадь сечения вихревой нити и угловая скорость могут меняться, но напряжение вихревой нити будет одно и то же. Она не может ни разорваться, ни исчезнуть.

Из теорем Гельмгольца следует: 1) вихревая нить и струйка жидкости геометрически подобны; 2) вихревая нить не может ни разорваться, ни исчезнуть; 3) напряжение вихревой нити всегда одно и то же; 4) на концах вихревой нити всегда будет пониженное давление, поэтому в свободном пространстве без стенок она всегда замкнется сама на себя и образует вихревой тор.

3. Теория функций пространственного комплексного переменного [8], [9]

Отсутствие наглядного геометрического представления реального физического пространства связано с отсутствием наглядных физических представлений о том, что означает понятие начала координат и как интерпретировать понятие координатной оси. С физической интерпретацией этих основных геометрических понятий связан кризис современной теоретической физики.

Физическая интерпретация начала координат в комплексном пространстве

Вершиной классической математики и математического анализа является теория функций комплексного переменного, основателем которой является французский математик О. Коши. Теория дошла до нашего времени почти в том виде, в котором она была создана. Значительно усилив мощь математического аппарата в инженерных расчетах, теория Коши оставила инженерный аппарат плоским расчетным. Для перехода к описанию пространственных физических процессов и явлений требуется введение в аппарат дополнительных координат, которые не соответствуют определению пространственной точки и окрестности ее, которая заложена в теории Коши. В теоретической физике, например, вводят матрицы, которые ближе к программному обеспечению, чем к математическому аппарату.

Теоремы Коши об изолированных точках и вычетах, а также взаимосвязь точек на плоскости комплексных координат дают основание на пересмотр абстрактного понятия точки. Рассмотрим последовательно: линию, плоскость, пространство.

Линия рассматривается как одномерное пространство, как и делают современные исследователи. Однако, как только на линии ставится точка ноль, как начало координат, что означает на инженерном языке привязку этой линии к реальному пространству, назвать линию одномерным пространством означает допустить грубейшую ошибку. Переход по линии из -¥ через точку 0 к +¥ нельзя не обогнув 0 по дужке и совершив оборот на угол j=±p (рис.8). Можно игнорировать этот факт, называя линию одномерным пространством, но можно утверждать, что линия терпит разрыв в точке в начале координат, какой бы минимальный радиус дужки e®0 не был, либо это уже не одномерное пространство.

Далее рассматриваем установившееся понятие двумерного (плоского) пространства. Если плоскость рисуется без начала координат, то это понятие не несет физического смысла. Если плоскость привязана к реальному пространству, то в ней фиксируется начало координат. В этом случае логика предыдущих рассуждений вступает в силу. Окрестность нуля не принадлежит этому двумерному миру. Окрестность нуля выколотое двумерное пространство (рис.9). Определение ноль имеет неопределенный аргумент 0=0ℓ^ij, физически означает, что плоскость проколота лучем, исходящим из другого измерения. Последнее и утверждает, что плоскость несет в себе элемент пространства.

Рис. 8 Рис. 9

Нельзя пройти точку ноль по прямой, не обогнув ее по дужке в его окрестности. Можно радиус дужки устремить к нулю, однако физическая сторона и в этом случае не меняется. Определение нуля как 0=0ℓ^ij в физических расчетах дает возможность игнорировать аргумент в точке ноль до тех пор как ноль не становится критической точкой. Простейшую кривую на плоскости окружность нельзя стянуть в точку около критической точки.

Продолжая эту логическую цепочку, восстановим к плоскости не линию, как это делает классическая математика, а цилиндрическую трубочку радиуса окрестности нуля. Сфера в таком пространстве является сферой с проколотыми вершинами. Пространство внутри сферы между ее внутренней поверхностью и наружной поверхностью цилиндрической оси есть пространство другого измерения, чем пространство вне сферы и внутри изолированной оси.

Простейшей пространственной кривой будет кривая С₃ (рис.10). Кривая характеризуется двумя аргументами j, y и двумя радиусами: R - радиус сферы, r_e - радиус цилиндрической оси. Двигаясь по кривой С₃ аргумент j получает приращение 4p, аргумент y получит приращение 2p. На кривую С₃ можно натянуть поверхность без точек самопересечения и нельзя сжать без складок в плоскую кривую. Более сложные кривые имеют, выражаясь физическим языком, большее количество намоток по поверхности сферы и цилиндрической оси.

При такой геометрической интерпретации абстрактное понятие точки, линии, плоскости детализируется: точка есть сфера d радиуса, линия есть цилиндр e- радиуса, плоскость имеет e- толщину.

Сферические пространственные комплексные координаты имеют вид:

x=Rcosjcosa;

y=iRsinjcosa;

z=jRℓ^ijsina.

Третья координата имеет вращение вокруг оси (этот вариант не рассматривается в квантовой механике, а вводится другими условиями, чтобы результат соответствовал эксперименту).

Физическая интерпретация координатных осей.

Основным признаком декартовых координат и всех других, применяемых в исследованиях физических процессов, является то, что координатные оси имеют начало из одной точки и даже не из ее окрестности. Перенос системы координат из одной точки в другую, поворот осей координат и так далее, описывается около одной точки.

В теоретической физике физическое поле описывается одно- или много- компонентной функцией координат и времени, называемой функцией поля. В качестве переменных берутся величины, которые подчинены законам скалярной, спинорной, векторной и тензорной алгебр.

К полевым переменным теоретическая физика добавила метрический тензор пространства-времени. Теоретическая физика объясняет это определением естественной геометрии физического поля и выбором той или иной системы координат. Таким образом, совершив ошибки в самом начале исследований, делается попытка их исправления с помощью операций, не соответствующих числовым операциям. В результате потеряно самое главное - возможность исследовать структурирование пространства с ростом его размерности.

Для поиска естественной геометрии используются уравнения Гамильтона-Якоби, Фока, Шредингера. Условия, которые получают из этих уравнений, накладывают на метрический тензор и тем самым утверждают, что получена естественная геометрия. Однако это тоже порочный круг. Условия должны вытекать из интегральных теорем N-мерного пространства, наподобие условиям Коши-Римана в плоскости.

Расстояние между двумя точками в N-мерном пространстве это корень N-степени из многочлена, представляющего сумму произведений координат в комбинациях дающих N-степень. Система линейных уравнений, применяемая при преобразовании одной системы координат в другую той же размерности с теми же законами алгебры (коммутативного или некоммутативного умножения), имеет определитель как сумму произведений координат, степень которой отвечает размерности пространства. В комплексной плоскости и в комплексном пространстве определитель системы равен модулю комплексного числа возведенного для плоскости в квадрат, для пространства в степень рассматриваемого преобразования. Для четырехмерного пространства интервал равен корню четвертой степени из суммы произведений координат дающих в комбинации четвертую степень. В связи с этим никакими метрическими тензорами нельзя откорректировать интервал принятый в форме дедуктивного переноса его выражения как корня квадратного из многочлена, представляющего сумму квадратов комбинации координат.

Преобразования Лоренца показывают, что координатные оси пространственные и временные исходят из разных точек окрестности начала координат. Не поняв этого Пуанкаре, Минковский, Эйнштейн выбросили из исследований самую существенную часть математического аппарата, которая отвечает за полевую структуру материи. Аппарат, обладающий модулем, не равным нулю, остался, а та часть, которая отвечает за полевую материю и разложена по осям координат, образуя крутящие моменты, была выброшена в исходном состоянии исследований. Эта комплексная особенность пространства обуславливает кривизну пространства. Вследствие этого не удалось теорию довести до логического конца. Физические преобразования Лоренца требовали корректировки пространственно-временных координат. Однако этого не произошло, и из исследования была выброшена самая существенная часть - исследование формирования структуры с ростом размерности пространства.

Опишем, что дает комплексная пространственная алгебра и систему комплексных пространственных координат.

Комплексная плоскость определяет точку с e -окрестностью. Начало координат не является точкой, а является e -окрестностью нуля. В связи с этим третья координатная ось не является линией, а является цилиндрической поверхностью радиуса e. Понятие точки и координатных линий расширяются до понятий e -сфер и e -цилиндров. Если две координатные оси представляют цилиндры комплексных точек, то третья координатная ось представляет цилиндр с двойными стенками, между которыми расположены цилиндры предыдущей размерности. В этом комплексном пространстве модуль комплекса равен интервалу теории относительности Минковского, выведенный из преобразований Лоренца.

Таким образом, интервал теории относительности возникает и получается естественным образом через соблюдение законов классической алгебры и правильного построения системы координат. В таком пространстве нет линий как таковых, а есть спирали намотанные на e -цилиндры с переменной частотой витка. Ввиду малости e эти спирали воспринимаются как линии. В плоскости двух координатных цилиндров точка становится объемным объектом - сферой, проколотой изолированными направлениями. Пространство, заключенное внутри этих цилиндров, принадлежит пространству другого измерения. Функция, определенная в таком пространстве, соответствует физической трактовке суперпозиции волн. Взаимодействие объектов друг с другом рассматривается как взаимодействие пространств различной по величине размерности.

Четырехмерное пространство выступает как элементарное. Оно является элементарным блоком, заполняющим пространство любого числа измерений. В элементарном блоке векторы i и j равноправны.

Наличие в пространстве изолированной (выколотой) оси (e -цилиндра) трактуется как вихревой шнур естественной циркуляции.

Согласно физической трактовке комплексного пространства под микрочастицей понимается часть пространства, изолированного от остального поверхностью, натянутой без точек самопересечения на циркуляционную пространственную кривую С₃ и имеющего контакт с пространством другой по величине размерности через изолированные e -туннели.

Простейшая комплексная кривая комплексного пространства.

Контур С₃ является простейшим пространственным контуром (рис.10). Он состоит из кривой, идущей по внешней поверхности сферы, и кривой, идущей по внешней поверхности выколотой оси.

Дадим определение кривой С₃ в комплексном пространстве, которую назовем главной простой кривой в пространстве. Простой кривой в пространстве трех и четырех измерений будем называть кривую С₃, которая получается деформацией из плоской кривой длины 2pR₀, путем натягивания ее на сферу с выколотым e -туннелем так, что часть кривой, равная 2R_e, проходит через e-туннель, а остальная часть, равная 2pR₀-2R_e, проходит по поверхности сферы так, что сфера при фиксированном R₀ имеет наибольший радиус. При этом точка, проходящая один раз замкнутую кривую С₃, делает в e -туннеле и по поверхности сферы в исчислении по углу j два полных оборота 4p, а по углу y один оборот 2p.

Простейшей комплексной кривой в z -плоскости является окружность. Натянуть на окружность поверхность так, чтобы в ней был заключен объем, не представляется возможным. Кривая С₃ является простейшей пространственной кривой, на которую можно натянуть непрерывным образом без точек самопересечения поверхность так, чтобы внутри содержался объем.

Внутренний контур кривой С₃ можно деформировать так, что он пойдет по внутренней поверхности сферы, при этом образуется оболочка толщиной d. Оболочку можно увеличить до толщины S, как это показано на рис.11. в этом случае пространство будет заключено между двумя сферическими поверхностями, соединенными между собой цилиндрической поверхностью выколотой оси. Иными словами, в любом случае простейшей поверхностью становится тороидальная поверхность. Кривую С₃ можно стянуть в геометрически подобную кривую около изолированной точки (рис.11).

Общий случай показывает, что поверхностные интегралы по формуле Остроградского при общих условиях ее применения могут быть переведены в объемные интегралы. Эта поверхность должна содержать объем и образовывать тело. В конкретном случае это тор, или сфера с выколотым e -туннелем.

Рис. 10 Рис. 11

Из теории функций комплексного пространственного переменного следует: 1) простейшей пространственной кривой является кривая, на которую можно натянуть непрерывным образом без точек самопересечения поверхность так, чтобы внутри содержался объем, 2) этот объем образует тело, в конкретном случае это тор, или сфера с выколотым e -туннелем; 3) объемный объект - сфера, проколотая изолированным направлением, становится эквивалентом точки в классической геометрии, она является элементарным блоком, заполняющим пространство любого числа измерений.

Заключение

Сформулированы основные теоремы физико-математической модели комплексного энергетического пространства. Из этих теорем следует, что основным элементом физического пространства является вихреторовое образование, которое является элементарным блоком, заполняющим пространство любого числа измерений. В геометрической интерпретации это сфера с выколотым e -туннелем или же поверхность с выделенным направлением. Физическое пространство может рассматриваться: либо в виде множества, содержащего плотную упаковку элементарных блоков; либо как комплексное пространство, состоящее из комплексных элементов; либо как векторное поле. Наличие плотной упаковки элементарных блоков, т.е. объемных тел, указывает на то, что их относительное движение невозможно, а возможно только изменение ориентировки их выделенного направления. Т.к. выделенное направление физически означает момент силы вихреторового объекта, то сложение этих сил должно приводить к пространственной деформации элементарных блоков, а, следовательно, к деформации физического пространства. Отсюда следует замечательный вывод, что деформацию пространства можно отождествить с понятием материального тела и физического поля. Тогда меняется общепринятое представление о перемещении материальных тел в пространстве. Оно преобразуется в перемещение деформаций физического пространства при неизменности его структуры. Другими словами, происходит последовательная деформация элементарных блоков пространства при отсутствии их пространственного перемещения. Изменение общепринятых представлений о движении как пространственном перемещении деформаций (материальных тел и физических полей) в корне меняет гносеологию движений.

Вращательное движение жидкой частицы называется вихревым.

Примеры – смутный след за самолетом, струя воздушного и гребного винтов, смерч и т.д.

Вихревой линией называется линия, в каждой точке которой в данный момент времени вектор угловой скорости направлен по касательной:

По аналогии с линией тока уравнение вихревой линии:

Если линии тока и вихревые линии совпадают, т.е. совпадают векторы и , то такое движение называется винтовым.

Если через замкнутый контур в объеме вращающейся жидкости провести вихревые линии – получим вихревую трубку.

Вихревая трубка, заполненная вращающейся жидкостью, называется вихревым шнуром или вихрем.

Вихревой шнур бесконечно малого сечения называется вихревой нитью.

Возьмем отрезок вихревой нити. Площадь поперечного сечения нити , нормального к угловой скорости w.

Удвоенное произведение угловой скорости элементарного вихря и площади его поперечного сечения называется интенсивностью или напряженностью вихревой нити.

Вихревой шнур , составленный из бесконечного множества вихревых нитей, будет иметь интенсивность (напряженность), определяемую интегралом:

где: S – площадь поперечного сечения вихря.

Составляющие угловой скорости жидкой частицы определяются через разницу перекрестных производных линейной скорости:

Дата добавления: 2015-05-23