Пример 3.40

Ц,,(у)

Пример 3.39

В примере 3.37 мы предположили, что Т-норма, декартово произ­ведение и нечеткая импликация определяются с помощью операции mi-

х,,х₂

дЬ (У) =

х,,х₂

АЦ, (Х₂) Л Htf» (*!,Х₂,у) =

ш

^(У);

*

(Х₂) Л

(Х₂))]} Л Ц_в„ (у) =

= {sup[/i_A. (X!) л ц^ (х,)] л sup[^. (x₂) л ц^ (x₂)]} л ц_в„ (у) (₃.₂65)

Х-] Х₂

В результате

min

⁸¹

МЛ

В»

,) л я_Л. (х,)] л

(3.266)

Рис. 3.29. Иллюстрация к примеру 3.37.

Глава 3. Нечеткие множества и нечеткий вывод

3.9. Нечеткое управление

Рис. 3.30. Иллюстрация к примеру 3.38.

Рис. 3.31. Иллюстрация к примеру 3.39.

nimum. Теперь заменим эту операцию на произведение. В соответствии с формулой (3.238) получаем

Таблица 3.5. Способы определения операции фуззификации, Г-нормы, декартова произведения и нечеткой импликации из примеров 3.35 - 3.39

u „

X,Х₂

_i.

(3.268)

х₂

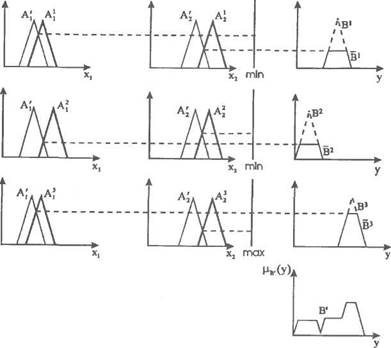
Функцию принадлежности нечеткого множества В' зададим согласно формулам (3.268) и (3.249). Графическая интерпретация нечет­кого вывода представлена на рис. 3.31.

В таблице 3.5 сгруппированы способы определения операции фуз-зификации, Г-нормы, декартова произведения и нечеткой импликации из примеров 3.35 - 3.39.

Ранее мы рассматривали правила вида (3.229). В этом примере два первых правила R<¹⁾ и R<²> представляют собой частные случаи выра­жения (3.229), тогда как правило R<³> содержит связку OR

Пример	Операция фуззификации	Т-норма декартова произведения	Определение нечеткой импликации	Правило	Рисунок
3.35	синглетон	min	min	min	3.27
3.36	синглетон	min	min	произ­ведение	3.28
3.37	не синглетон	min	min	min	3.29
3.38	не синглетон	min	min	произ­ведение	3.30
3.39	х-,- не синглетон х2- синглетон	произ­ведение	произ­ведение	произ­ведение	3.31

Глава 3. Нечеткие множества и нечеткий вывод

3.9. Нечеткое управление

R⁽¹⁾: IF (х₁ это a] AND х₂ это а\) THEN (у это В.,), R<²>: IF (_Х1 это д,² AND х₂ это а\) THEN (у это В₂), R<³>: IF (х₁ это Д³ OR х₃ это Д₂³) THEN (у это В₃).

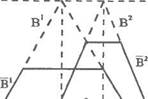
На рис. 3.32 показана графическая интерпретация нечеткого выво­да при условии, что 7-норма, декартово произведение и правило нечет­кой импликации имеют тип min. Обсуждаемая проблема решается и дру­гим способом. Для этого обратим внимание на то, что правило R<³⁾ можно представить в виде двух правил R⁽³⁾ и R ⁽⁴⁾:

R<³>: IF (_X1 это А?) THEN (у это В₃), R⁽⁴⁾: IF (х₃ это А\) THEN (у это В₃).

Мы получили правила R<¹>, R<²>, R⁽³⁾ и R⁽⁴⁾, которые представ­ляют собой частные случаи выражения (3.229). Читатель с легкостью вы-

ведет аналитическую форму функции принадлежности множества В', ба­зируясь на результатах примера 3.37.

3.9.1. 4. Блок дефуззификации

На выходе блока выработки решения формируется либо N нечет­ких множеств В" (случай 1, п. 3.9.1.3) с функциями принадлежности ^gk(y), k = 1, 2,..., Л/, либо одно нечеткое множество В¹ (случай 2, п. 3.9.1.3) с функцией принадлежности ц_в.(у). Встает задача отображения нечетких множеств В^к (либо нечеткого множества В') в единственное значение у е Y, которое представляет собой управляющее воздействие, подаваемое на вход объекта. Такое отображение называется дефуззифи-кацией (defuzzification), и реализуется оно в одноименном блоке.

Если на выходе блока выработки' решения формируется Л/ нечет­ких множеств В ", то значение у е Y можно рассчитать с помощью раз­личных методов.

1. Метод дефуззификации по среднему центру (center average defuzzification). Значение у рассчитывается по формуле

(3.269)

у^к

где у* -это точка, в которой функция р._Вк{у) принимает максимальное значение, т.е.

AV (У^к) = max n_Rk (у). (3.270)

Точка у^к называется центром {center) нечеткого множества В^.

На рис. 3.33 представлена идея этого метода для Л/ = 2. Обратим внимание, что значение у не зависит от формы и носителя функции при­надлежности ц_Вк(у).

2. Метод дефуззификации по сумме центров (center of sums defuzzification). Значение у рассчитывается следующим образом:

(3.271)

Рис. 3.32. Иллюстрация к примеру 3.40.

Глава 3. Нечеткие множества и нечеткий вывод

3.9. Нечеткое управление

Ив-(У)

Рис. 3.34. Иллюстрация метода центра тяжести.

у¹ у у² у

Рис. 3.33. Иллюстрация метода дефуззификации по среднему центру.

Если выходное значение блока выработки решения представляет собой единственное нечеткое множество В', то значение у можно опре­делить с применением следующих двух методов.

3. Метод центра тяжести (center of gravity method, center of area method). Значение у рассчитывается как центр тяжести функции принад­лежности 1Л_В (у), т.е.

\

ymaxjUg^y)

у = -

(3.272)

Jmax p^ (у)

при условии, что оба интеграла в приведенном выражении существуют. На рис. 3.34 иллюстрируется способ определения значения у по методу центра тяжести.

4. Метод максимума функции принадлежности. Значение у рас­считывается в соответствии с формулой

(3.273)

yeY

при условии, что ц_в. (у) - это унимодальная функция. Этот метод не учитывает форму функции принадлежности, что иллюстрируется на рис. 3.35.

Дата добавления: 2015-06-04