Решим задачу (1) в EXCEL

Итак, нахождение решения игры в смешанных стратегиях может быть сведено к решению пары двойственных задач линейного программирования.

Согласно лекции 6 получена пара двойственных задач (1) и (2). Напомним, что, решив одну из них, например, симплекс-методом, мы автоматически найдем решение другой.

Воспользуемся теоремой Неймана.

Напомним, что суммы вероятностей равны 1.

Решить игру, заданную платежной матрицей

И товар Т1 иТ2. При этом товар Т1 должен быть закуплен на сумму 421тыс. руб., а Т2 - на сумму 579 т. руб. Прибыль не зависимо от поведения соперника составит 321052 руб. То же можно сказать и для игрока В.

§ 10 Сведение матричных игр с нулевой суммой к задачам линейного программирования

Покажем, на примере, как игру двух лиц с нулевой суммой можно свести к решению пары двойственных задач линейного программирования и решить, например, симплекс-методом (табличным или в среде EXCEL). Отметим [4], что и любая задача линейного программирования может быть сведена к матричной игре.

Пример:

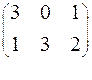α= 1, β= 2 → игра без седловой точки.

Пусть (р₁, р₂) – смешанная стратегия игрока А, (q₁, q₂, q₃) – смешанная стратегия игрока В.

Для игрока А:

введем обозначения:

y₁ = р₁/v, y₂ = р₂/v. (Заметим, что v = 1/(y₁ + y₂)).

Задача примет вид:

3y₁ + y₂ ≥ 1

3y₂ ≥ 1

y₁ + 2y₂ ≥ 1

G = y₁ + y₂ → min (1)

Для игрока B:

Обозначим х₁ = q₁/v, х₂ = q₂/v, x₃= q₃/v. Заметим, что

v= 1/(x₁ + x₂+ x₃).

Задача примет вид:

3x₁ + x₃ ≤ 1

x₁ + 3x₂ +2x₃ ≤ 1

F = x₁+ x₂+ x₃ → max (2)

у₁ = 1/5, у₂= 2/5, v= 1/0,6

р₁ = (1/5)*(5/3)=1/3, р₂ = 2/3.

Пример:

Имеются две конкурирующие фирмы А и В. Фирма А в будующем году может производить 4 новых модели айфонов:А1,А2,А3,А4. Конкурент В также может производить 4 новых модели: В1,В2,В3,В4. Платежная матрица (прибылерованияй) фирмы А имеет вид:

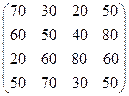
Как рациональнее всего поступить каждой фирме, чтобы получить наибольшую прибыль?

Для фирмы А записываем задачу линейного программирования:

70у₁+60у₁+20у₁+50у₁≥ 1

30у₁+50у₁+60у₁+70у₁≥ 1

20у₁+40у₁+80у₁+30у₁≥ 1

50у₁+80у₁+60у₁+50у₁≥ 1

G = y₁+ y₂+ y₃+ y₄ → min

Экономический пример (курсовая работа)

Металлургический консорциум (игрокА) с целью улучшения финансового состояния должен принять решение об инвестиции 10 млн. в банк

(игрок В).

Совет директоров консорциума рассматривает возможность открытия $ счетов на сумму 2 млн., 3 млн. и 5 млн. $.

Какие установит процентные ставки противостоящий консорциуму банк заранее неизвестно. Возможные варианты по указанным вкладам таковы: 12%, 6 % и 8 % или 9%, 10 % и 7 %, соответственно. У игрока В, таким образом, две чистых стратегии.

Естественно, консорциум стремится увеличить свою прибыль, а банк минимизировать выгоду консорциума. Методами теории игр найти оптимальные стратегии консорциума, а также банка. Какой ожидаемый доход может получить консорциум?

Чистые стратегии игрока А (консорциума) перечислим и опишем в таблице:

Чистые стратегии игрока А	1 тип вклада (2 млн.)	11 тип вклада (3 млн.)	111 тип вклада (5 млн.)
	2,2,2,2,2	-	-
	2, 2, 2
	2, 2	3, 3
	2, 2
		3, 3, 3
			5, 5

Пояснение: 1-я чистая стратегия предполагает открытие 5 вкладов по 2 млн., 2-я -3 вкладов по 2млн и одного по 3 млн. (напомним - всего в наличии 10 млн.). Дальнейшая структура таблицы понятна!

Чистые стратегии игрока В: выплачивать проценты по первому варианту или по второму варианту.

Дата добавления: 2015-06-04